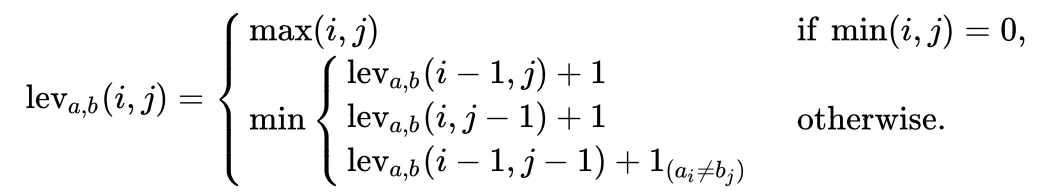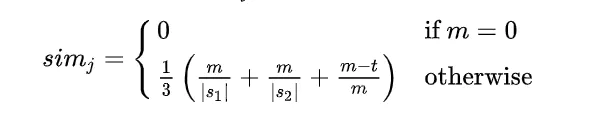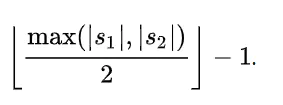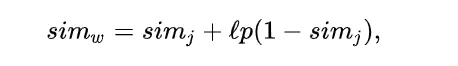BlogPapers

SummerSec

View on GitHub

相似度算法调研

前言

相似度算法故名思义，就是判断两个件事物是否是存在相似相似性，通常我们比较多是一些字符串、文本文件。相似度算法其实很多都使用过，很经典的案例毕业论文全网匹配相似度，也就是我们常说的查重。

对两个较短的字符串，我们在人工判断是否具有相似性的时候，通常很快就能做出判断。

For Example:

我是中国人，在中国生活！

我是美国人，在美国生活！

这两个句话，就只存在两个字的差异。大家可以试着想想如何判断这两句是否相似的？

但如果使用统计字符串的方式很容易就在一些特定的语意的情况下很容易产生较大的差异的，比例说：

在中国，每一个人爱着国家。

中秋节，每一个人爱吃月饼。

在这情况下使用统计字符串的方式就可能误报了太大了，但这种情况在本文中不考虑，这属于是自然语言处理的范围，这个领域在全球都是还是一个比较难的研究课题。

相似度算法介绍

莱文斯坦-编辑距离(Levenshtein)

编辑距离（Minimum Edit Distance，MED），由俄罗斯科学家 Vladimir Levenshtein 在1965年提出，也因此而得名 Levenshtein Distance。

编辑距离的本质思想就是将两个中的一个字符串转化成另一个字符串最少需要编辑单个字符的个数。譬如，”kitten” 和 “sitting” 这两个单词，由 “whoami” 转换为 “whoiam” 需要的最少单字符编辑操作有：

  1. whoami → whoimi (substitution of “a” for “i”)
  2. whoimi → whoiai (substitution of “m” for “a”)
  3. whoiai → whoiam (substitution of “i” for “m” at the end)

因此，”whoami”和”whoiam”的编辑距离为3。

表示为 ![lev_{a,b}( a , b )](https://math.jianshu.com/math?formula=lev_%7Ba%2Cb%7D(%7Ca%7C%2C%20%7Cb%7C))

实现算法：

我们将两个字符串a,b 的 Levenshtein Distance 表示为![lev_{a,b}( a , b )](https://math.jianshu.com/math?formula=lev_%7Ba%2Cb%7D(%7Ca%7C%2C%20%7Cb%7C)) ，其中![ a ](https://math.jianshu.com/math?formula= a ) 和 ![ b ](https://math.jianshu.com/math?formula=%7Cb%7C) 分别对应 a,b 的长度。那么，在这里两个字符串a,b 的 Levenshtein Distance，即![lev_{a,b}( a , b )](https://math.jianshu.com/math?formula=lev_%7Ba%2Cb%7D(%7Ca%7C%2C%20%7Cb%7C)) 可用如下的数学语言描述：

img

1. 定义 lev_{a,b}(i, j) 指的是 a 中前 i 个字符和 b 中前 j 个字符之间的距离。为了方便理解，这里的i,j可以看作是a,b的长度。这里的字符串的第一个字符 index 从 1 开始（实际因为在表上运算的时候字符串前需要补 0），因此最后的编辑距离便是 i = |a|, j = |b| 时的距离： lev_{a,b}(|a|, |b|)

2. 当 min(i, j) = 0 的时候，对应着字符串a 中前 i 个字符和 字符串b 中前 j 个字符，此时的 i,j 有一个值为 0 ，表示字符串 a 和 b 中有一个为空串，那么从 a 转换到 b 只需要进行max(i, j)次单字符编辑操作即可，所以它们之间的编辑距离为 max(i, j)，即 i, j 中的最大者。

3. 当 min(i, j) \ne 0 的时候，lev_{a,b}(|a|, |b|) 为如下三种情况的最小值：
1.lev_{a,b}(i-1, j) + 1 表示 删除 a_i
2.lev_{a,b}(i, j-1) + 1 表示 插入 b_j
3.lev_{a,b}(i-1, j-1)+1_{(a_i \ne b_j)} 表示 替换 b_j

1_{(a_i \ne b_j)} 为一个指示函数，表示当 a_i = b_j 的时候取 0 ;当 a_i \ne b_j 的时候，其值为 1。

Hamming

两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：

1011101 与 1001001 之间的汉明距离是 2。

2143896 与 2233796 之间的汉明距离是 3。

“toned” 与 “roses” 之间的汉明距离是 3。

最简单汉明算法实现

func (h *Hamming) CompareUtf8(utf8Str1, utf8Str2 string) float64 {
	count := 0

	l1 := utf8.RuneCountInString(utf8Str1)
	max := l1

	l2 := utf8.RuneCountInString(utf8Str2)
	if max < l2 {
		max = l2
	}

	for i, j := 0, 0; i < len(utf8Str1) && j < len(utf8Str2); {
		size := 0
		r1, size := utf8.DecodeRune(StringToBytes(utf8Str1[i:]))
		i += size

		r2, size := utf8.DecodeRune(StringToBytes(utf8Str2[j:]))
		j += size

		if r1 != r2 {
			count++
		}

	}

	return 1 - (float64(count)+math.Abs(float64(l1-l2)))/float64(max)
}

Dice’s coefficient

Jaro

1、Jaro distance/similarity 对于两个字符串s1和s2，它们的Jaro 相似度算法由下面公式给出：

img

其中： ①|s1|和|s2|表示字符串s1和s2的长度。 ②m表示两字符串的匹配字符数。 ③t表示换位数目transpositions的一半。

m的计算表达式为：

img

JaroWinkler

Jaro-Winkler similarity是在Jaro similarity的基础上，做的进一步修改，在该算法中，更加突出了前缀相同的重要性，即如果两个字符串在前几个字符都相同的情况下，它们会获得更高的相似性。该算法的公式如下：

img

其中： ①simj 就是刚才求得的Jaro similarity。 ②l表示两个字符串的共同前缀字符的个数，最大不超过4个，取值范围[0,4]。 ③p是缩放因子常量，它描述的是共同前缀对于相似度的贡献，p越大，表示共同前缀权重越大，最大不超过0.25。p默认取值是0.1

Cosine

余弦相似度，相关原理就是高中学过的空间向量定理，两个向量夹角的角度。但余弦相似度得计算词出现频率，如果用分词的效率不高，并且计算量，内存开销都会很大。于是我想到采用base64编码的方式，因为base64编码的字符串同一个字符是相同的，也等价的计算词语出现的频率。然后将base64标准字符串进行余弦计算。

img

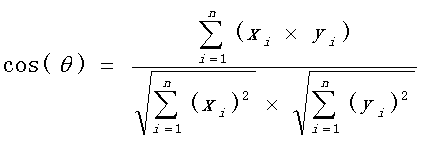
SimHash

传统的Hash算法只负责将原始内容尽量均匀随机地映射为一个签名值，原理上仅相当于伪随机数产生算法。传统的hash算法产生的两个签名，如果原始内容在一定概率下是相等的；如果不相等，除了说明原始内容不相等外，不再提供任何信息，因为即使原始内容只相差一个字节，所产生的签名也很可能差别很大。所以传统的Hash是无法在签名的维度上来衡量原内容的相似度，而SimHash本身属于一种局部敏感哈希算法，它产生的hash签名在一定程度上可以表征原内容的相似度。

　　我们主要解决的是文本相似度计算，要比较的是两个文章是否相识，当然我们降维生成了hash签名也是用于这个目的。看到这里估计大家就明白了，我们使用的simhash就算把文章中的字符串变成 01 串也还是可以用于计算相似度的，而传统的hash却不行。我们可以来做个测试，两个相差只有一个字符的文本串，“你妈妈喊你回家吃饭哦，回家罗回家罗” 和 “你妈妈叫你回家吃饭啦，回家罗回家罗”。

　　通过simhash计算结果为：

　　1000010010101101111111100000101011010001001111100001001011001011

　　1000010010101101011111100000101011010001001111100001101010001011

　　通过传统hash计算为：

　　0001000001100110100111011011110

　　1010010001111111110010110011101

　　大家可以看得出来，相似的文本只有部分 01 串变化了，而普通的hash却不能做到，这个就是局部敏感哈希的魅力。

​ SimHash的难点感觉是在分词和加权，分词处理之后，加权操作目前没有很好的解决方法。分词的话，如果是中英文的都有的情况也很难处理，比例说网页的源代码。对于分词这部分，我目前简单将文本进行base64编码，然后将粗暴的以四个字符分为一组。对于加权这块，我是统计每组出现的概率进行加权。

总结

​ 本节主要是讨论一下相似度算法的实现算法，目前本来中所有的算法都均已开源到GitHub，仓库地址 https://github.com/antlabs/strsim 。这个仓库并不是我的，我只是一个贡献者，目前算法的实现还没有结果大量测试，欢迎大家讨论并提出改进算法想法💡。

参考